Hoare C.A.R. (1969) An Axiomatic Basis for Computer Programming. COMMUNICATIONS OF THE ACM Verification. vol 12: page 576–580
译者:陈思源
本文隶属于”每天一篇计算机 Paper”系列博客,更多内容请点击这个链接。
本系列博客均非完整译文,如需阅读完整文章,请访问相关图书馆订阅。
ABSTRUCT
在本文中,为探索计算机程序的逻辑基础,我们尝试使用了一些首先应用于几何学研究,后来扩展到其他数学分支的技术。这包括阐明公理集和可用于证明计算机程序的属性的推理规则。我们给出了这些公理和规则的例子,并且展示了简单定理的形式证明。最后,我们讨论了对这些主题的研究可能会同时带来的理论和实践方面的重要优势。
In this paper an attempt is made to explore the logical foundations of computer programming by use of techniques which were first applied in the study of geometry and have later been extended to other branches of mathematics. This involves the elucidation of sets of axioms and rules of inference which can be used in proofs of the properties of computer programs. Examples are given of such axioms and rules, and a formal proof of a simple theorem is displayed. Finally, it is argued that important advantages, both theoretical and practical, may follow from a pursuance of these topics.
INTRODUCTION
计算机程序是一门精确的科学,因为程序的所有属性以及在任何给定环境中执行它的所有后果原则上都可以通过纯粹的演绎推理从程序本身的文本中找到。演绎推理包含对有效公理集应用有效的推理规则。因此,阐明作为计算机程序推理基础的公理和推理规则是可取和有趣的。公理的确切选择在某种程度上取决于编程语言的选择。出于说明的目的,本文仅限于一种非常简单的语言,它本质上是所有当前面向过程的语言的一个子集。
Computer programming is an exact science in that all the properties of a program and all the consequences of executing it in any given environment can, in principle, be found out from the text of the program itself by means of purely deductive reasoning. Deductive reasoning involves the application of valid rules of inference to sets of valid axioms. It is therefore desirable and interesting to elucidate the axioms and rules of inference which underlie our reasoning about computer programs. The exact choice of axioms will to some extent depend on the choice of programming language. For illustrative purposes, this paper is confined to a very simple language, which is effectively a subset of all current procedure-oriented languages.
Formal Language Definition
高级编程语言(例如 ALGOL,FORTRAN 和 COBOL)通常旨在在具有不同大小,配置和设计的各种计算机上进行实现。 已经发现一个严重的问题是,为确保所有实现者之间的兼容性,这些语言的定义要足够严格。由于兼容性的目的是促进用语言表达的程序的交换,实现这一目的的一种方法是坚持语言的所有实现都应“满足”推理的公理和推理规则,这些证据是表达程序属性的证据的基础。在语言中,除非出现硬件故障,否则将完成基于这些证明的所有预测。实际上,这相当于接受公理和推理规则作为语言意义的最终明确规范。
A high level programming language, such as ALGOL, FORTRAN, or COBOL, is usually intended to be implemented on a variety of computers of differing size, configuration, and design. It has been found a serious problem to define these languages with sufficient rigour to ensure compatibility among all implementors. Since the purpose of compatibility is to facilitate interchange of programs expressed in the language, one way to achieve this would be to insist that all implementations of the language shall “satisfy” the axioms and rules of inference which underlie proofs of the properties of programs expressed in the language, so that all predictions based on these proofs will be fulfilled, except in the event of hardware failure. In effect, this is equivalent to accepting the axioms and rules of inference as the ultimately definitive specification of the meaning of the language.
除了为实现的正确性提供立即且可能甚至可证明的标准之外,用于定义编程语言语义的公理技术看起来像 ALGOL 60 报告的形式语法,因为它很容易被该语言的实现者和相当顶尖的用户理解。只有通过在单个文档(可能甚至证明是一致的)中弥合这种不断扩大的沟通差距,才能从正式的语言定义中获得最大的优势。
Apart from giving an immediate and possibly even provable criterion for the correctness of an implementation, the axiomatic technique for the definition of programming language semantics appears to be like the formal syntax of the ALGOL 60 report, in that it is sufficiently simple to be understood both by the implementor and by the reasonably sophisticated user of the language. It is only by bridging this widening communication gap in a single document (perhaps even provably consistent) that the maximum advantage can be obtained from a formal language definition.
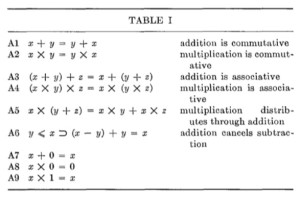
使用公理化方法的另一个巨大优势是公理提供了一种简单而灵活的技术,可以使语言的某些特定方面无需定义,例如,整数范围,浮点精度和溢出技术的选择。这对于标准化目的是绝对必要的,否则语言将无法在不同的硬件设计上有效地实现。因此,编程语言标准应该由一组普遍适用性的公理组成,并且从一组描述实施者所面临的选择范围的补充公理中进行选择。第2节给出了为此目的使用公理的一个例子。
Another of the great advantages of using an axiomatic approach is that axioms offer a simple and flexible technique for leaving certain aspects of a language undefined, for example, range of integers, accuracy of floating point, and choice of overflow technique. This is absolutely essential for standardization purposes, since otherwise the language will be impossible to implement efficiently on differing hardware designs. Thus a programming language standard should consist of a set of axioms of universal applicability, together with a choice from a set of supplementary axioms describing the range of choices facing an implementor. An example of the use of axioms for this purpose was given in Section 2.
形式语言定义的另一个目标是帮助设计更好的编程语言。ALGOL 60 语法的规律性,清晰度和易于实现,可能至少也有部分归因于其定义使用了精美的规范技术。公理的使用可能在”语义学”领域产生类似的优势,因为似乎可以通过一些“不言而喻”的公理来描述一种语言,这种公理可以相对容易地构建,这种语言可能比一种具有许多模糊公理的语言,难以用于证明。此外,公理使语言设计者能够非常简单直接地表达他的一般意图,而不需要描述通常伴随算法的大量细节。最后,公理可以用很大程度上彼此独立的方式表达,这样设计师就可以在一个公理或一组公理上自由地工作,而不用担心与语言的其他部分的意外交互影响。
Another of the objectives of formal language definition is to assist in the design of better programming languages. The regularity, clarity, and ease of implementation of the ALGOL 60 syntax may at least in part be due to the use of an elegant formal technique for its definition. The use of axioms may lead to similar advantages in the area of “semantics,” since it seems likely that a language which can be described by a few “self-evident” axioms from which proofs will be relatively easy to construct will be preferable to a language with many obscure axioms which are difficult to apply in proofs. Furthermore, axioms enable the language designer to express his general intentions quite simply and directly, without the mass of detail which usually accompanies algorithmic descriptions. Finally, axioms can be formulated in a manner largely independent of each other, so that the designer can work freely on one axiom or group of axioms without fear of unexpected interaction effects with other parts of the language.